Flat Earth theory was debunked 2,000 years ago, explains Carl Sagan

More than 2,000 years ago, a Greek mathematician proved that the surface of the Earth was curved and not flat.

That mathematician was Eratosthenes, who was a geographer, poet, astronomer, and music theorist. So, how did a mathematician debunk the modern-day theory that the Earth is flat 2,000 years ago? As explained by Carl Sagan in the above video, Eratosthenes planted a stick in the ground in Syene, a city south of Alexandria, and another in Alexandria. The distance between the two sticks was 800 kilometers.

Now, if both of the sticks that were planted casted an identical shadow at the same time of day, it would suggest that the surface of Earth is flat. However, Eratosthenes found that the shadow casted by one of the sticks wasn't identical to the other, in fact, the difference between the shadow casted in Alexandria, and the one in Syene was 7 degrees.

2

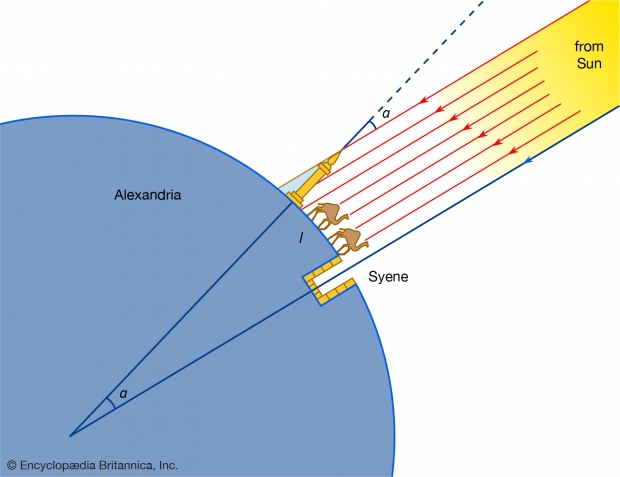
With this measurement, Eratosthenes was able to find Earth's circumference - 7.2 degrees is 1/50 of 360 degrees - 800 times 50 equals 40,000 kilometers. Satellites today measure Earth's circumference at 40,030km. More than 2,000 years ago, a man with a keen mind for mathematics and two sticks managed to prove that the Earth's surface is curved and not flat. Yet, people are still debating the topic today.